# SimNDT2 > Revised version. New: - Numpy output format - JSON model format - Improved GUI (Parameter tree can be modified)  Software simulator written in Python with the following features: Parallel implementation of Viscoelastic EFIT (Elastodynamic Finite Integration Technique): - 2D P/SV: 2th spatial-time order (Elastic/Viscoelastic Media) - Parallel codes using OpenCL via PyOpenCL - Capable to simulate Ultrasonic NDT inspection systems: Pulse-echo, Through-Transmission, Linear Scan, Radial Scan, Tomography - Capable to generate various type of geometric scenarios - Capable to export simulation results in .Mat-File Format ---- Ultrasonic NDT Simulator with engine core based on the Elastodynamic Finite Integration Technique (EFIT) (P/SV: 2th spatial-time order) for Elastic/Viscoelastic media to model the wave propagation in 2D for viscoelastic and elastic materials [1]. The SimNDT has a very friendly and easy to use GUI. This software is able to simulate different ultrasonic inspection methods as Pulse-echo, Through-Transmission, Linear Scan, as well as Scan and Tomography. In addition, it is capable to generate or import different types of geometric scenarios and export simulation results in mat-file format for further processing. To improve the performance of this technique the software was implemented using the standard for parallel programming of heterogeneous systems, OpenCL (Open Computing Language). It works in both multicore processors and GPU's (Intel, NVIDIA or AMD) Please before using it and depending of your system, install your required OpenCL Drivers: https://developer.nvidia.com/cuda-downloads https://software.intel.com/en-us/articles/opencl-drivers https://developer.amd.com/amd-accelerated-parallel-processing-app-sdk/ [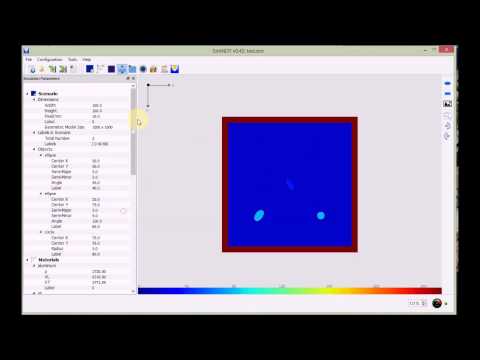](https://youtu.be/yQCY2OSdJfY) [1] M. Molero-Armenta, U. Iturrarán-Viveros, S. Aparicio and M.G. Hernández, Optimized OpenCL implementation of the Elastodynamic Finite Integration Technique for viscoelastic media, Comput Phys Comm 185 (2014) 2683-2696. ___